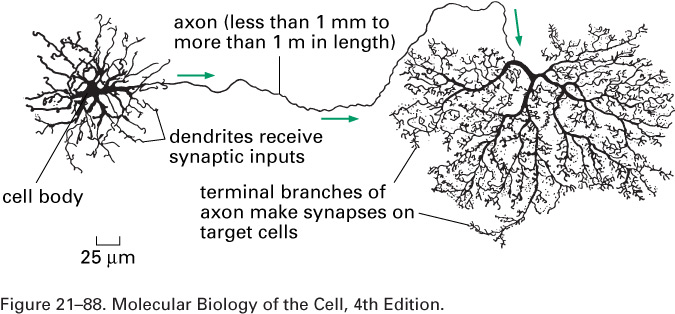
The dendrites receive incoming signals; the axon and its branches carry signals to other cells.
Transporters, mainly sodium-potassium
pumps, water channels, and gated ion channels, mainly the potassium leak channel,
control the osmotic
pressure of a cell and maintain the concentrations of sodium,
potassium, and chloride at about 14, 140, and 14 mM inside the cell
when it is immersed in a bath in which the Na+, K+,
and Cl- concentrations are 140, 3, and 146 mM. The
resulting resting voltage across the membrane is
ΔV = V2 - V1 = Vinside - Voutside
= -70 mV,
and the electric field E points into the cell.
A nerve cell, or neuron, consists of a cell body with
branching dendrites and a long axon, which may
range from 1 mm to 1 m in length, with its terminal branches which make
synapses with target
cells. Axon diameters run from less than a micron to more than a
millimeter.

The dendrites receive incoming
signals; the axon and its branches carry
signals to other cells.
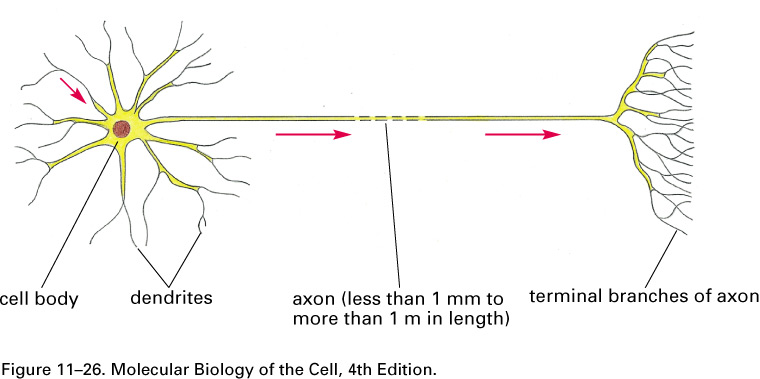
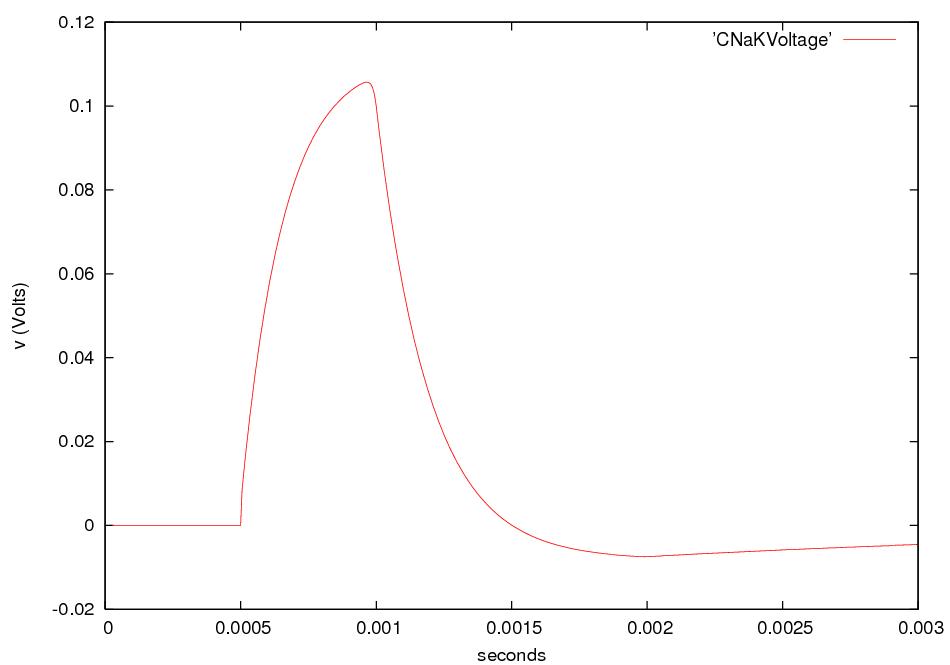
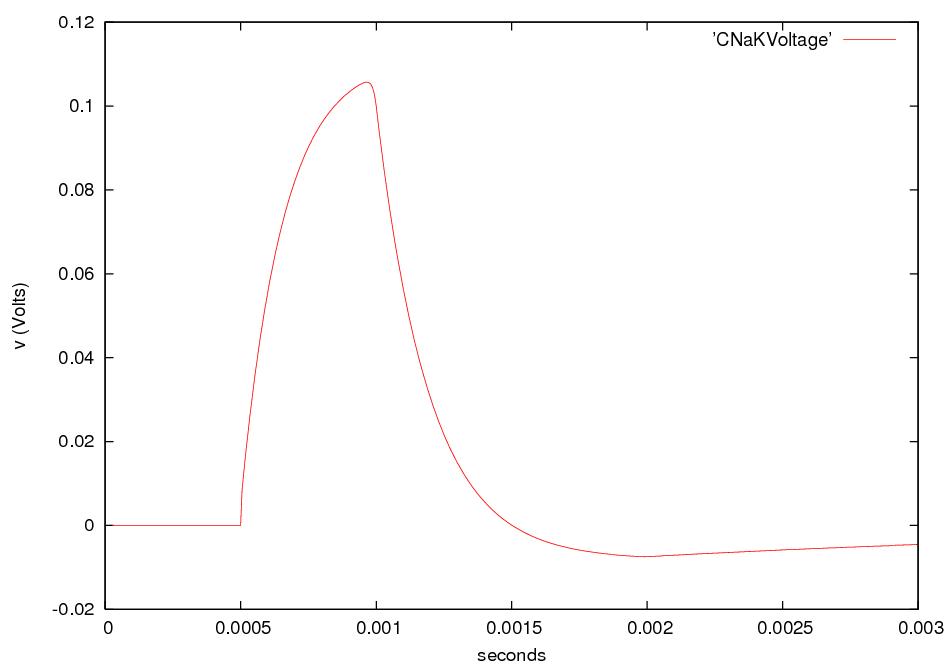
Nerve signals are called action potentials.
They are pulses of about 1 ms in which ΔV is + 40 mV instead of the
resting potential of -60 or -70 mV.
Thus the action potential is a change
in ΔV of about 100 mV.
These pulses travel with little change in shape at constant speeds in
the range of
0.1 to 120 m/s.
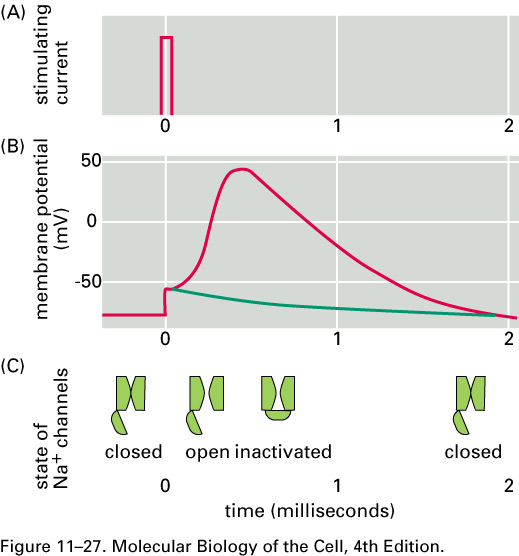
For about 1 ms after an action
potential
passes a given part of an axon,
that part of the axon is hard to stimulate.
This pause is called the refractory
period. After the
action potential passes a given part of an axon, ΔV recovers,
overshoots, and then returns to its
resting value in about 5 ms.
This behavior is called afterhyperpolarization
.
Neural contacts occur at synapses, most often when a branch of an
axon touches a dendrite or the body of a target cell.
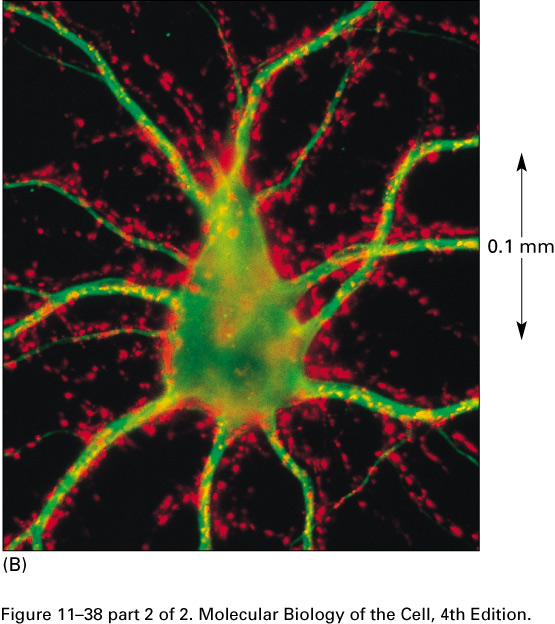
In this micrograph of the cell body
of a motor neuron of a spinal cord,
the axon terminals are red and the cytoskeleton is green:
The gap between the end of an axon branch and a dendrite (or a spine on
a dendrite) of a target neuron is between about 10 and 30 nm; it is
called the synaptic cleft.
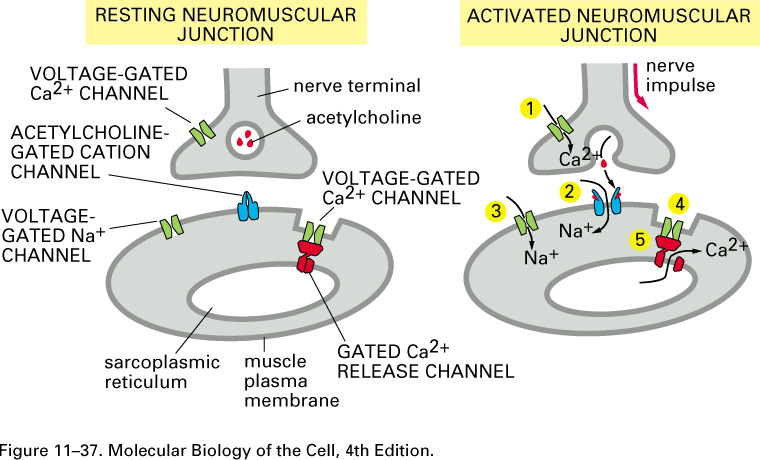
Here are cartoons of a resting and
an active synapse:
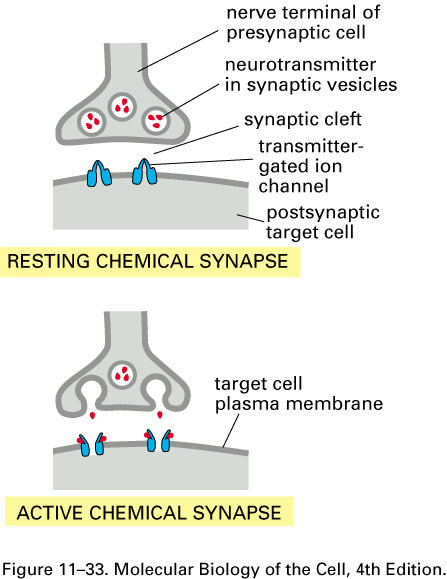
Neurotransmitters, such as
acetylcholine, serotonin, GABA, glycine, and glutamate, can open transmitter-gated sodium, potassium, and
chloride channels. The excitatory
neurotransmitters open sodium
channels, and the resulting influx of sodium depolarizes the membrane, making ΔV = V2 - V1
= Vinside - Voutside more positive and
possibly leading to an action potential. The inhibitory neurotransmitters
open potassium or chloride channels. The efflux of
potassium further polarizes the membrane, making ΔV = V2 - V1
more negative. The
concentration of Cl- is 10 times higher outside the cell,
and so when the chloride
channels open, the influx of Cl-
tends to further polarize
the membrane. So both potassium
and chloride
transmitter-gated channels tend to stop the generation of action
potentials.
Mammalian brains add extra non-NMDA
glutamate-receptor sodium channels after repeated
entries of Ca2+ thru the
NMDA receptor:
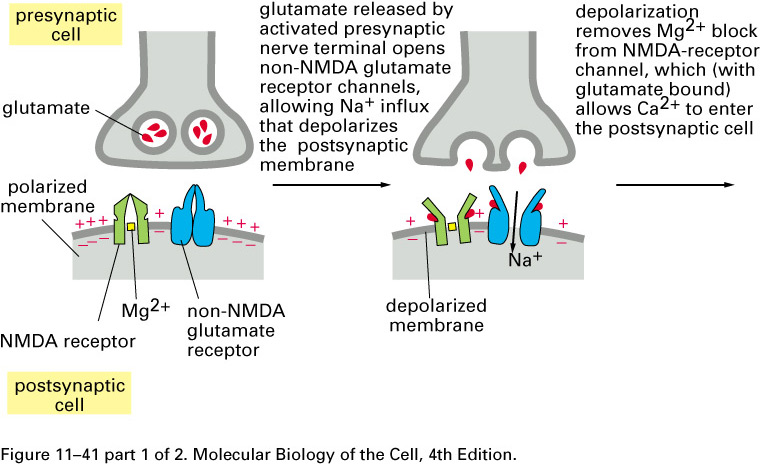
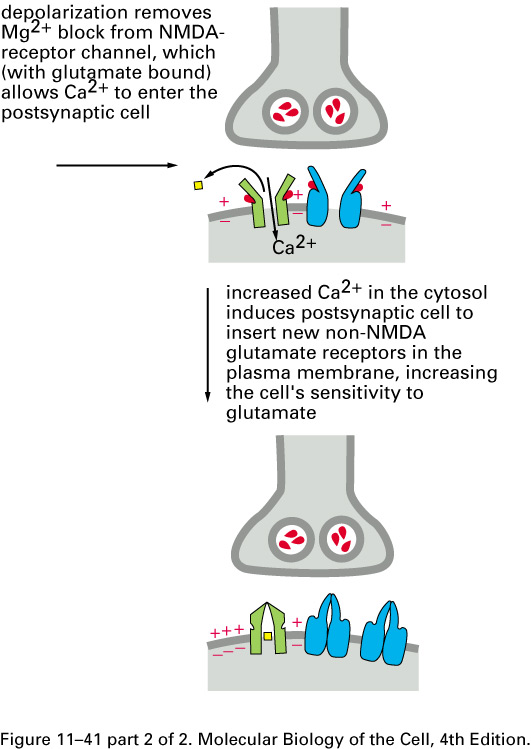
Here is a scanning electron
micrograph of a neuromuscular junction in a
frog:
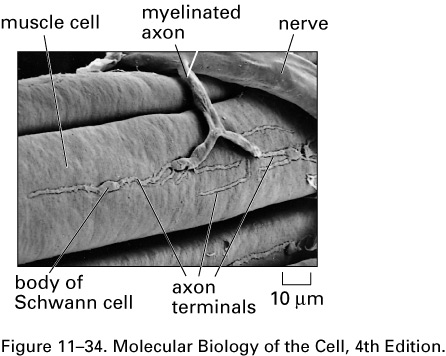
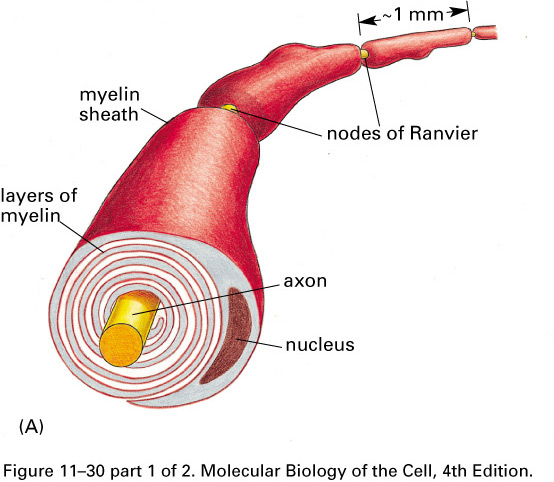
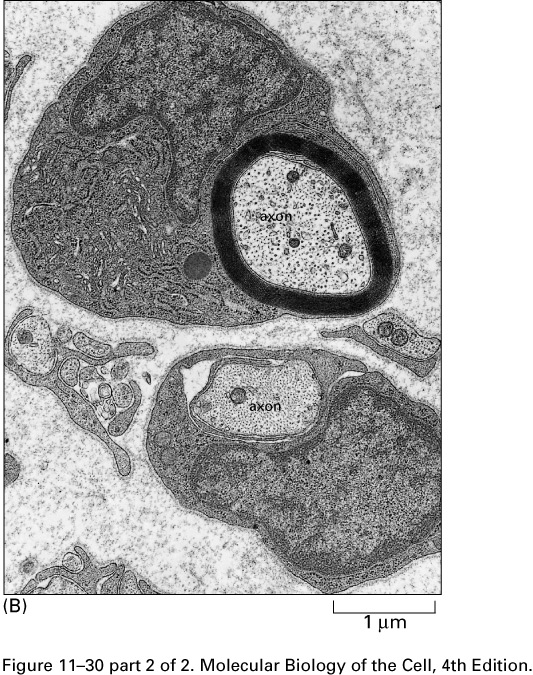
Glial cells (Schwann cells and
oligodendrocytes) wrap their plasma membranes about the axons of many
of the neurons of vertebrates
forming myelin sheaths
.
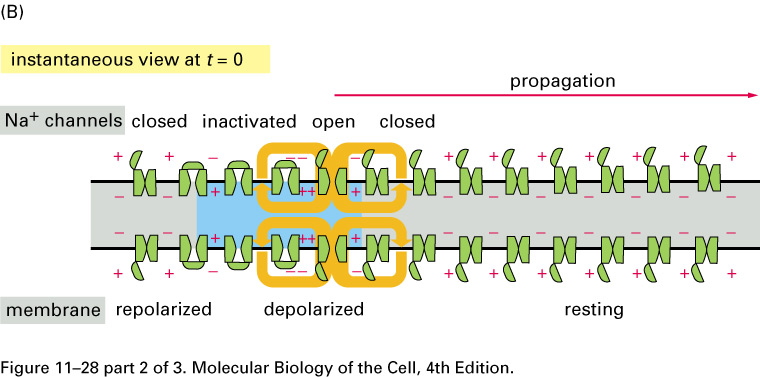
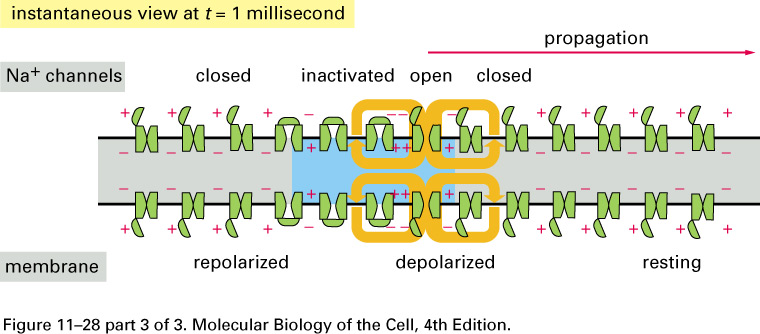
The voltage-gated sodium channels
are concentrated in gaps in the myelin,
the nodes of Ranvier,
about 1 mm apart. The action potential
jumps from node to node, traveling faster
than in unmyelated axons.
The disease multiple sclerosis
destroys some of the myelin in the
central nervous system, slowing down action potentials with devastating
results.
The human brain has about 100
billion (1011) neurons.
Here is a drawing by Golgi of a small part
of the olfactory bulb (sense of smell) of a dog's brain:
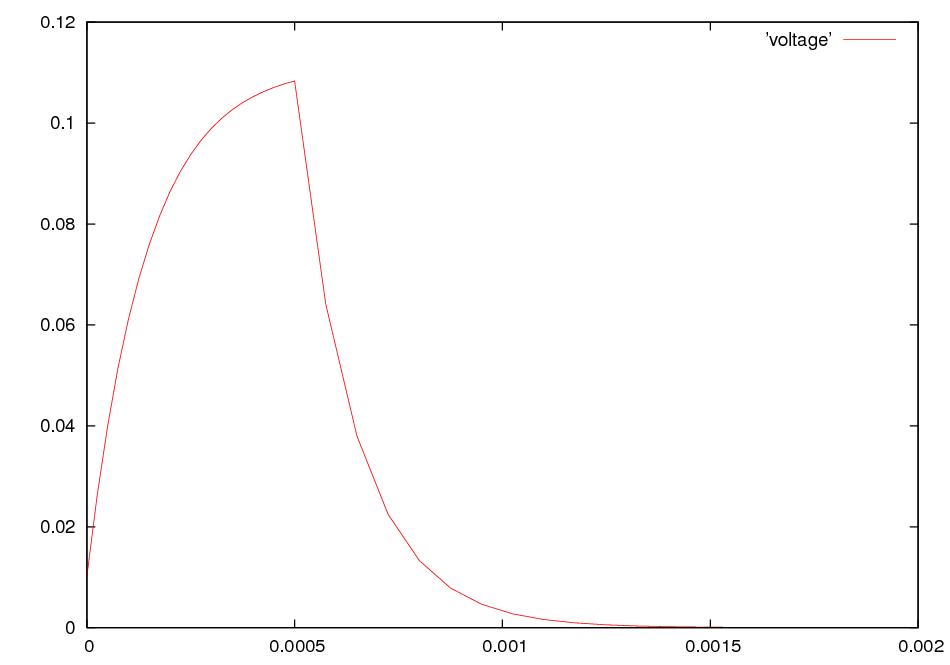
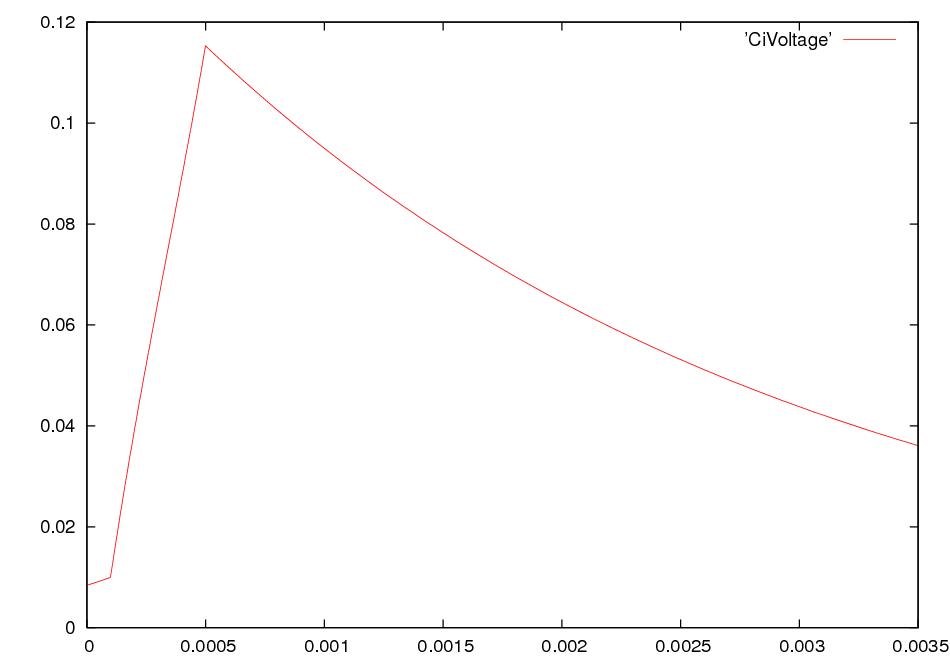
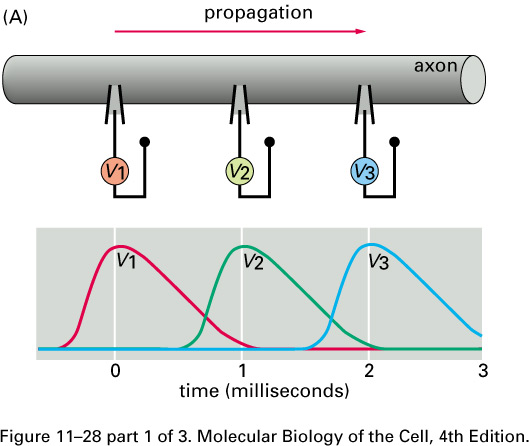
What happens if we electrically stimulate a nerve cell? If we slightly decrease ΔV throughout a small patch of the membrane of a nerve cell and then measure ΔV at points several mm away, we find a reduced decrease ΔV that fades with time and distance. The cell resets its ΔV to - 60 mV, and at distances of 100 mm, the change in ΔV is very small. A neuron recovers from a slight depolarization. If we slightly increase Δ V in a small patch of membrane, then at points several mm away ΔV will show an increase that fades with distance and time. The cell resets its ΔV to -60 or -70mV. A neuron recovers from a slight hyperpolarization. This passive spread of electrical signals is called electrotonus. In both depolarization and hyperpolarization, the magnitude of the spreading change in ΔV is proportional to the stimulus: the response is graded.
But if we depolarize the membrane
by more
than about 10 mV, then we can set in motion
an action potential.
The huge difference in the response
is
due to voltage-gated Na+
channels:
How do we describe action potentials
mathematically? We note
that the voltage drop across
the membrane ΔV = V2 - V1 is the same for
all three species, Na+, K+, and Cl-.
This voltage is the sum
ΔV = IiRi
+ VNi
(12.1)
of the Ohmic drop IiRi
and the
Nernst potential
ViN = - (kT/zie)
ln(ci2/ci1) .
(11.1)
Here Ri = 1/(A gi) is
the resistance, A the area, and gi
the conductance, and Ii =
jq,i A is the current of species i.
Next, we will ignore the myelin
and the sodium-potassium pumps. Instead, we'll just assume the
resting values
of the bulk concentrations and of ΔV mentioned above. In any case,
these values
remain fairly constant for about 6 105
s
after the pumps are stopped. We'll denote the quasi-steady value
of ΔV by V0.
If gi is the
conductance of
species i,
then the current of that species
will be (V0
- ViN)gi.
Since there is no build-up of charge
inside the axon, the sum of these currents
must vanish
∑i
(V0
- ViN)gi
= 0.
(12.2)
Let gtot denote the sum
of the three conductances
gtot = ∑i
gi.
Then the quasi-steady membrane
voltage is
V0 = ∑i
(gi/gtot) VNi
(12.3)
which is called the chord conductance formula. The
relations gK+ = 25 gNa+ = 2
gCl- tell us that gCl- =
12.5 gNa+, and so that
gtot = 38.5 gNa+. The Nernst
potentials from Table 11.1 are
VNK+ = -75 mV,
VNNa+
= 54 mV, and
VNCl-
= -59 mV. So the chord conductance formula gives
V0 = (25/38.5)(-75) + (1/38.5) 54 +
(12.5/38.5)(-59)
mV
= -66 mV
which is not very different from the
value
of -72 mV found in Eq.(11.12).
The axon's membrane is a
capacitor.
When a voltage V is applied across it,
opposite charges q and -q appear within
a Debye length of the membrane.
If C is the capacitance of the membrane,
then the charge q and the voltage V are related by
q = CV.
(12.4)
If the voltage is changing with
time,
then by differentiating the preceding equation,
we find
(dq/dt) = I = C (dV/dt).
(12.5)
This current is called a capacitive current.
The capacitance C is proportional to
the area A of the axon,
C = A C.
Experimentally,
C
= 10-2 F m-2
= 1 µ F cm-2.
We still have not modeled the
voltage-gated
sodium channels, so we don't expect
to get much of an action potential
with the present model, but let's push
ahead anyway.
Consider a cylindrical slice of radius a
and thickness dx of an axon
that points in the x-direction.
Let Ix(x) be the current
flowing into the cylindrical slice at x.
Then -Ix(x+dx) is the
current flowing into the cylindrical slice at x+dx.
The radial current flowing out is 2 π a dx jq,r plus
the pile-up rate
2 π a dx C (dV/dt).
Since charge is conserved, we have
Ix(x) -Ix(x+dx)
= - (dIx(x)/dx) = 2 π a (jq,r + C (dV/dt))dx.
(12.6)
We can relate the current Ix
to the voltage difference
ΔVx = V(x+0.5dx)
-V(x-0.5dx)
and the resistance of the axoplasm
(the axon's cytoplasm)
R = dx/(π
a2 κ)
by the formula
ΔVx = Ix R.
Thus we get
Ix = -
(V(x+0.5dx) -V(x-0.5dx))/R
=
- π a2 κ (dV/dx).
(12.6.5)
If we now put Eq.(12.6.5) into (12.6),
then we find
π a2κ (d2V/dx2)
= 2 π a ( jq,r + C (dV/dt) )
(12.7a)
or
aκ(d2V/dx2)
= 2 ( jq,r + C (dV/dt) )
(12.7b)
which is the cable equation.
Now V0 is the
quasi-steady voltage across the
membrane
— the voltage that gives no net
radial flux jq,r.
So the outward radial current flux is
jq,r = (V - V0)gtot .
Now let
v(x,t) = V(x,t) -V0 .
And let's define the axon's
space constant as
λ = (aκ/2gtot)1/2
(12.8a)
and its time constant as
τ = C/gtot.
(12.8b)
With these definitions and
assumptions,
the cable equation becomes the
linear cable equation
λ2 (d2v/dx2)
-τ (dv/dt) = v.
(12.9)
Letting v(x,t) = exp(-t/τ)
w(x,t),
we find that (12.9) becomes
(λ2/τ)
(d2w/dx2) =
dw/dx
which is the diffusion equation we studied in Sec.(4.6.5).
Using its solutions, we have with N a normalization constant
v(x,t) = N exp(-t/τ) t-1/2
exp(-x2/(4tλ2/τ)
(12.10)
which is the passive-spread solution.
With a = 0.5 mm, gtot = 5 m-2Ω-1,
C =10-2F m-2, and
κ = 3 Ω-1 m-1,
we get
λ 12 mm (12.11a)
and
τ = 2 ms.
(12.11b)
Here is a cartoon that describes both voltage-gated
sodium channels
and (slightly better) voltage-gated potassium
channels:
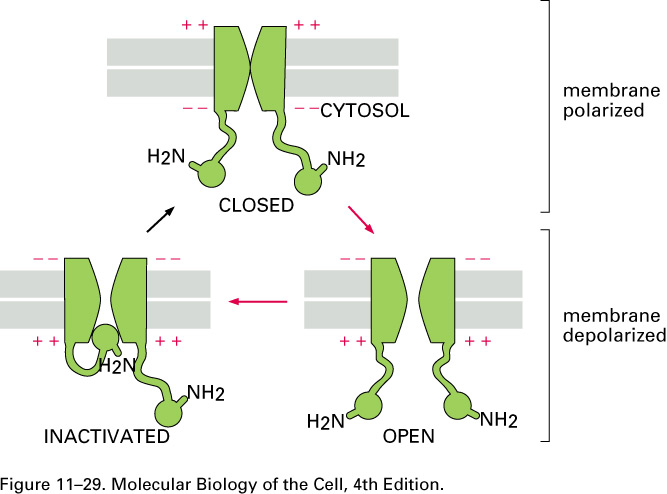
When the membrane is depolarized by more than about 10
mV, the voltage-gated
sodium channels open. When enough of them
are open on a given patch of the axon's membrane, the
sodium conductance momentarily jumps from the value of Table 11.1,
which was gNa+
= 0.04 gK+
to
gK+ = 0.05 gNa+
= 2gCl-
(12.14)
that is, the sodium conductance
jumps from
gNa+
= 0.04 gK+
to gNa+ = 20 gK+
which is to say by a
factor of 25 x 20 =
500. Sodium ions come flooding in when the sodium
channels are open.
The voltage-gated potassium
channels are slower than the voltage-gated
sodium
channels to respond to changes in the voltage
across the membrane. They open only after this voltage V = V2
- V1 has reached its maximum of about +40 mV.
The action potentials of some muscle, egg, and endocrine cells depend upon voltage-gated calcium channels.
We seek a traveling-wave
solution, that is, one of the form
V(x,t) = V(t - x/s)
where s is the speed of the
wave. The text has a tilde on the second V and uses a Greek theta for the
speed, but I am not good enough at html to be so fancy. Now the
spatial derivative of this traveling wave is
dV(x,t)/dx = dV(t - x/s)/dx = (-1/s) dV(t - x/s)/dt
(12.145)
and its second spatial derivative is
d2V(x,t)/dx2
= (1/s2)
d2V(t - x/s)/dt2
. (12.146)
If we put this traveling-wave solution
into the cable
equation (12.7b), then we find
which is an ordinary, not
a partial, differential equation.
Our simplified
voltage-gating hypothesis is that the outward radial current jq,r is
jq,r
=
∑i ( V - ViN
) gi(V).
(12.17)